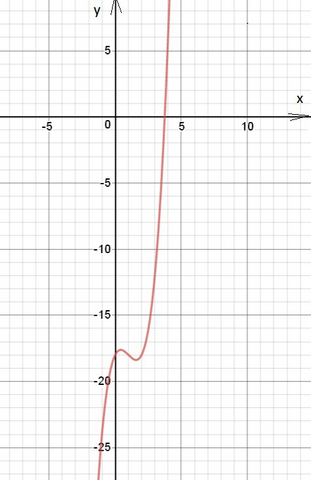
Уравнение имеет один корень.
Исследуем функцию у=х³-3х²+2х-18.
y`=3x²-6x+2
y`=0
3x²-6x+2=0
D=(-6)²-4·3·2=36-24=12
x=(6-2√3)/6=1-(√3/3) x=(6+2√3)/6=1+(√3/3) - точки экстремума функции, так как проходя через эти точки производная (квадратичная функция меняет знаки).
___+____(1-(√3/3))____-____(1+(√3/3))___+__
х=1-(√3/3)- точка локального максимума.
х=1=(√3/3) - точка локального минимума.
Причем локальный максимум отрицательный.
См. график функции. Кривая пересекает ось ох в единственной точке между 3 и 4, ближе к 4.
Алгебраическое решение в применением формул Кардано. Но это курс высшей алгебры.