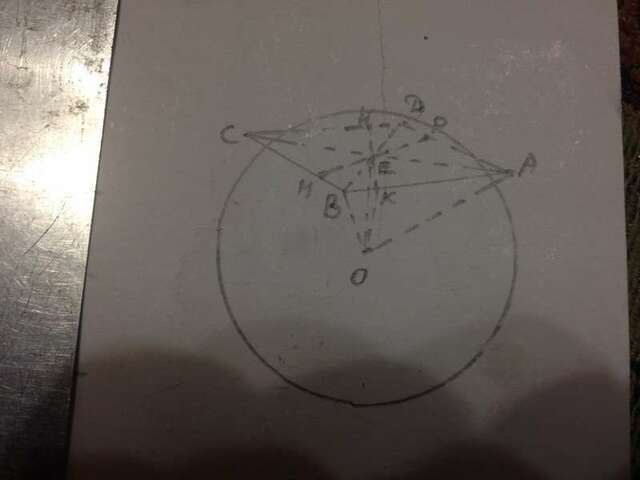
АВСД - ромб, К, М, Н и Р - точки касания сферой сторон АВ, ВС, СД и АД соответственно. КН и МР - высоты ромба, АС=16 см, ВД=12 см, ОК=ОМ=ОН=ОР=8 см.
Сторона ромба по т. Пифагора: АВ=√[(АС/2)²+(ВД/2)²]=√(8²+6²)=10 см.
В прямоугольном тр-ке АВЕ высота ЕК=ЕА·ЕВ/АВ=8·6/10=4.8 см.
В тр-ке ОЕК ОЕ²=ОК²-ЕК=√(8²-4.8²)=6.4 см.
В тр-ке OEA ОА=√(ОЕ²+ЕА²)=√(6.4²+8²)=√104.96=8√41/5≈10.2 см - это ответ.
В тр-ке ОЕВ ОВ=√(ОЕ²+ЕВ²)=√(6.4²+6²)=√76.96=2√481/5≈8.8 см - это ответ.
ОА=ОС, ОВ=ОД.