По свойству параллельных плоскостей:
Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны. ⇒
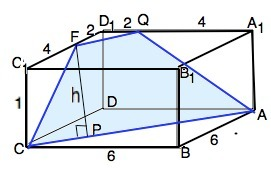
FQ-линия пересечения искомой плоскости с верхним основанием призмы. FQ||AC
По условию СF:FD1=2:1 ⇒
СD1:FD1=3:1
FD1=6:3=2
∆ FD1Q~∆ ADC – прямоугольные, их стороны параллельны.
AC=AD:sin45°=6√2
Из подобия ∆ FD1Q~∆ ADC следует ∠D1FQ=DCA=45°
FQ=FD1:sin45°=2√2
CFQA - равнобедренная трапеция. FP⊥AC, FP- высота
Высота равнобедренной трапеции, проведенная из тупого угла, делит большее основание на отрезки, меньший из которых равен полуразности оснований, больший – их полусумме.
СР=(АС-FQ):2=2√2
FC²=CF²+CC1*=17
Из прямоугольного ∆ СFP по т.Пияагора
FP=√(CF²-CP²)=√(17-8)=3
S(CFQA)=FP•(FQ+AC):2=3•(2√2+6√2):2=12√2 (ед площади)