Две окружности радиусов 9 см и 3 см касаются внешним образом в точке А,через которую проходит их общая секущая ВС.Найдите длину отрезка АВ если АС=5 см
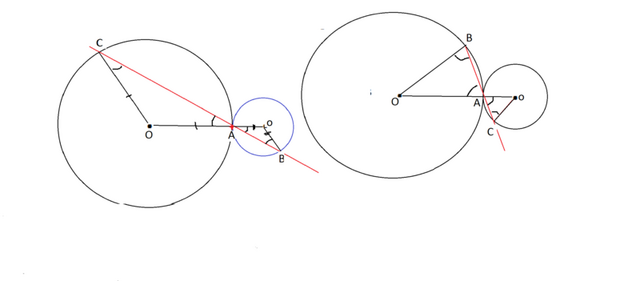
Сделаем рисунок к задаче.
Соединим центры окружностей. Точка ихкасания находится на линии, осединяющей центры.
У задачи есть два варианта решения.
1)Точка С находися на большей окружности.
Тогда АВ является хордой меньшей окружности.
Соединив центры окружности и концы хорд, образованных секущей ВС,
получим подобные треугольники СОА и АоВ.
Они подобны по трем углам.
Углы при А - вертикальные и потому равны.
Углы С и В - углы при основании равнобедренных треугольников с боковыми сторонами - радиусами каждой окружности, и потому они равны углам при А.
Так как углы при основаниях АС и АВ этих треугольников равны, их центральные углы также равны.
Из подобия треугольников АОС и АоВ, коэффициент подобия которых
9:3=3, находим, что
СА:АВ=3
СА:5=3
СА=15 см
-------------------------
2) Точка С находится на меньшей окружности.
Тогда при том же коэффициенте подобия
АВ:АС=3
5:АС=3
АС=5/3=1⅔ см