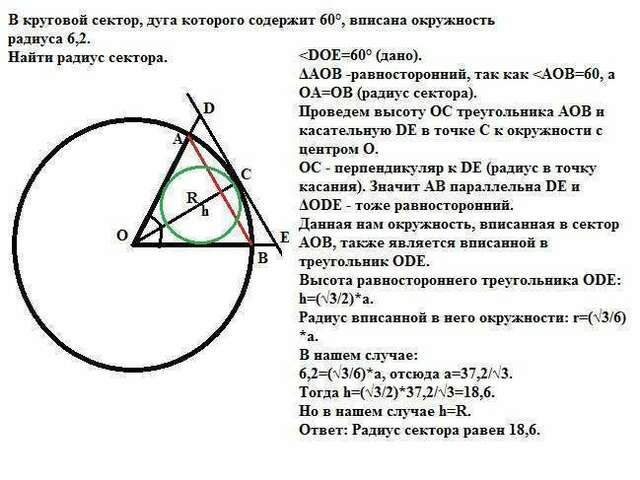
ΔАОВ -равносторонний, так как Проведем высоту ОС треугольника АОВ и касательную DE в точке С к
окружности с центром О.
ОС - перпендикуляр к DE (радиус в точку касания). Значит АВ параллельна DE и ΔОDE - тоже равносторонний.
Данная нам окружность, вписанная в сектор АОВ, также является вписанной в треугольник ОDE.
Высота равностороннего треугольника ОDE: h=(√3/2)*a.
Радиус вписанной в него окружности: r=(√3/6)*a.
В нашем случае:
6,2=(√3/6)*a, отсюда а=37,2/√3.
Тогда h=(√3/2)*37,2/√3=18,6.
Но в нашем случае h=R(искомый радиус).
Ответ: Радиус сектора равен 18,6.