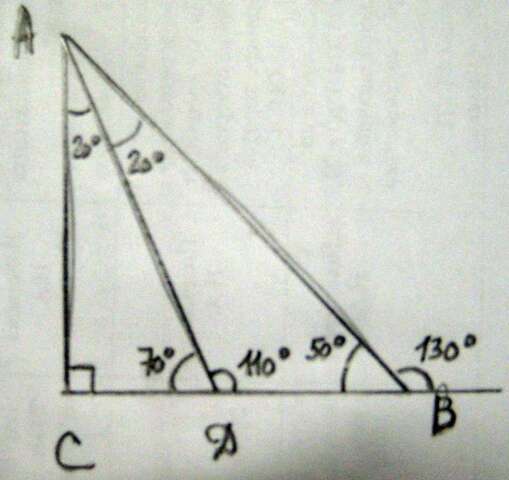
∠CDA=180-110=70° (углы CDA и ADC - смежные, а сумма смежных углов равна 180°)
∠CAD=180-70-90=20° (сумма углов треугольника ACD равна 180°, угол С - прямой)
∠DAB=∠CAD=20° (так как AD - биссектриса угла А)
∠DBA=180-110-20=50° (сумма углов треугольника ADB равна 180°)
Внешний угол при вершине В = 180 - 50 = 130° (углы DBA и внешний угол при вершине В - смежные, а сумма смежных углов равна 180°)