В трапеции ABCD (AD ∥ BC, AD > BC) ** диагонали AC выбрана точка E так, что BE ∥ CD....

Question

В трапеции ABCD (AD ∥ BC, AD > BC) на диагонали AC выбрана точка E так,
что BE ∥ CD. Площадь треугольника ABC равна 10. Найдите площадь
треугольника DEC.

Answer 1

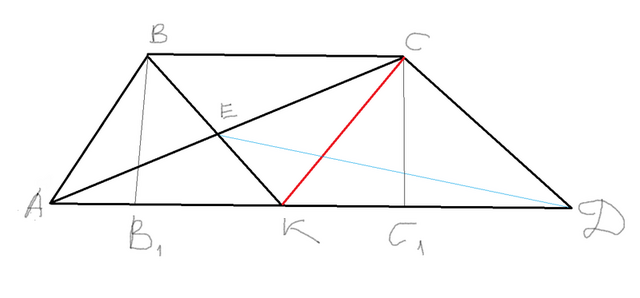
рисунок в приложении

 

Треугольники DEC и DKC равновеликие,т.к. у них общее основание CD , а высоты, проведённые из вершин E и K на основание CD равны, так как КЕ||CD.

 

 

 

Треугольники ABC и CDK равновелики, т.к. у них равны основания ( DK = BC ) и высоты, проведённые из вершин A и C , поскольку BC || AD . Следовательно, треугольники ABC и DEC также равновелики.   

 

Значит площадь DEC равна 10 см²

---