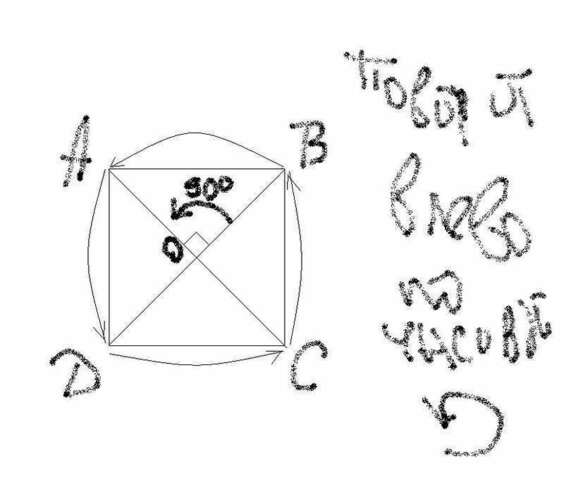Пусть АВСD - данный квадрат(AB=BC=CD=AD), О - точка пересечения диагоналей АС и BD
Так как диагонали квадрата равны, и точкой пересечения делятся пополам, то
АО=ВО=СО=DO
Диагонали квадрата пересекаются по пряммым углом (т.е. под углом 90 градусов), а это означает, что при повороте квадрата вокруг точки пересечения его диагонали т.О (влево)
т.А - перейдет в т.D
т.D - перейдет в т.C
т.C - перейдет в т.B
т.B - перейдет в т.A
(треугольник AOB- перейдет в треугольник AOD,
треугольник AOD- перейдет в треугольник COD,
треугольник COD- перейдет в треугольник BOC,
треугольник BOC- перейдет в треугольник AOB)
а значит квадрат ABCD - перейдет в квадрат ABCD - аналогично при повороте на 90 градусов (вправо)
Доказано