Два круга радиусами по 8 см имеют общую хорду 8√3 см. а) найдите площадь общей части кругов, б) площадь фигуры, образованной всеми точками этих кругов
------------
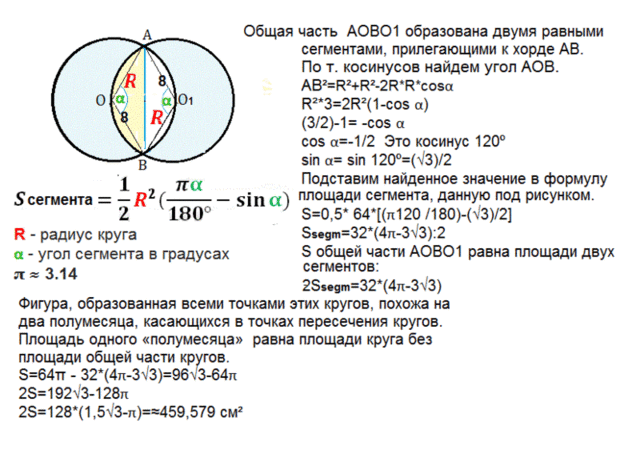
Рассмотрим данный в приложении рисунок.
Общая часть кругов АОВО1 образована двумя равным сегментами, прилегающими к общей хорде АВ.
Площадь сегмента найдем по формуле:
S=0,5 R²*[(πα /180)-sin α],
где
R - радиус круга.
α - угол сегмента в градусах,
π ≈ 3.14
По т. косинусов найдем угол АОВ.
АВ²=R²+R²-2R*R*cosα
R²*3=2R²(1-cos α)
(3/2)-1= -cos α
cos α=-1/2 Это косинус 120º
sin α= sin 120º=(√3)/2
Подставим найденное значение в формулу площади сегмента.
S=0,5* 64*[(π120 /180)-(√3)/2]
S=32*(4π-3√3)
:2
Площадь общей части АОВО1 равна площади двух сегментов
:
2S=32*(4π-3√3)
Фигура, образованная всеми точками этих кругов, похожа на два полумесяца, касающихся в точках пересечения кругов.
Площадь одного «полумесяца» равна площади круга без площади общей части кругов.
S=64π - 32*(4π-3√3)=96√3-64π
2S=192√3-128π
2S=128*(1,5√3-π)=
≈459,579 см²