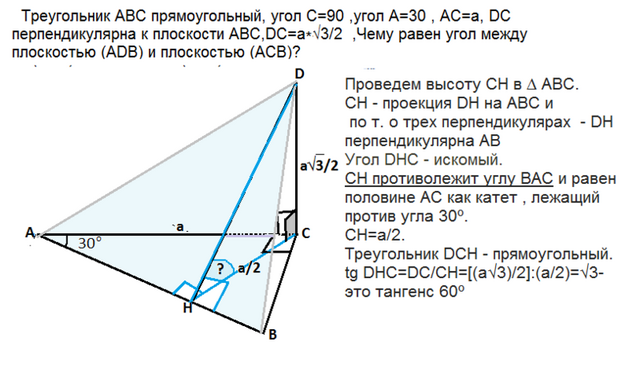
Треугольник АВС-прямоугольный, угол С =90º, угол А равен 30º. АС=а, DС перпендикулярно плоскости АВС. DС=а√3)/2. Чему равен угол между плоскостями АDВ и АСВ?
-----
Искомый угол - двугранный.
Чтобы найти величину двугранного угла или угла между плоскостями, нужно построить линейный угол и найти величину этого линейного угла.
Линейный угол двугранного угла - угол, образованный двумя лучами на образующих его плоскостях, проведенными перпендикулярно к одной точке на линии пересечения этих плоскостей, т.е ребру двугранного угла.
Проведем высоту СН в ∆ АВС.
СН - проекция DН на АВС и по т. о треух перпендикулярах
DH перпендикулярна АВ
Угол DHC - искомый.
В треугольнике АСН катет СН противолежит углу А и равен половине его гипотенузы АС как катет противолежащий углу 30º.
СН=а/2.
tg ∠DHC=DC/CH=[(a√3)/2]:(a/2)=√3- это тангенс 60º