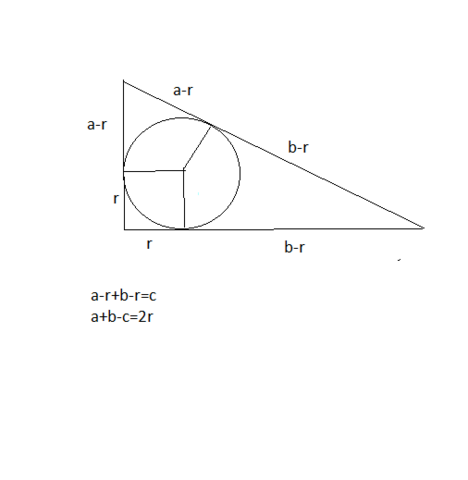
По свойству касательных к окружности, проведенных из одной точки, отрезки касательных равны.
см. рисунок в приложении
Поэтому
a+b-с=2r
r=(a+b-c)/2 ПОЛЕЗНАЯ ФОРМУЛА
так как гипотенуза прямоугольного треугольника является диаметром описанной окружности, прямой угол опирается на диаметр, то
c=2R - диаметр окружности, описанной около прямоугольного треугольника
2=(a+b-10)/2 ⇒ a+b=14
По теореме Пифагора
a²+b²=10²
Решаем систему уравнений
b=14-a
a²+(14-a)²=10²
2a²-28a+96=0
a²-14a+48=0
a=6 или a=8
b=8 b=6
S(Δ)=a·b/2=6·8/2=24 кв. см