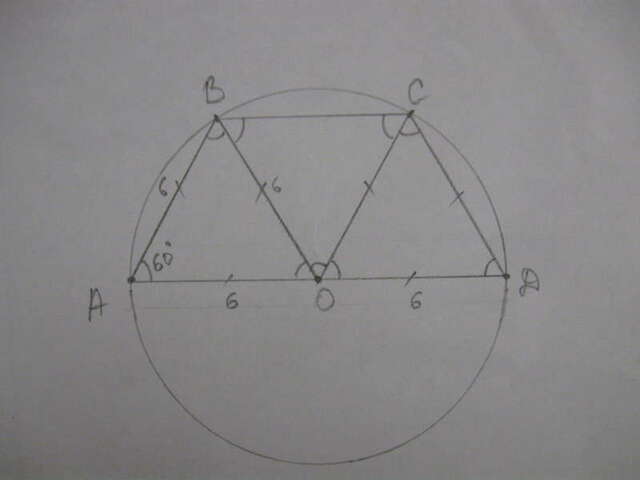
Рисунок к задаче смотри в прикрепленном файле.
Как известно, вписать в окр-сть можно только РАВНОБЕДРЕННУЮ трапецию!
1) Соединим точки В и С с центром окр-сти О. Получим треугольники АВО, ВОС и ОСД.
2) Рассмотрим тр-к АВО: Он равнобелренный (АО=ВО=R), угол при основании по условию равен 60 градусов, значит угол АВО=А=60, а угол АОВ=180-(60+60)=60 градусов. Получили равносторонний тр-к со стороной АО=ВО=АВ=R=6 см. Итак, боковые стороны трапеции равны по 6 см. Аналогично, тр-к СОД равносторонний.
3) Рассмотрим тр-к ВОС. Он равнобедренный (ВО=СО=R), а угол при вершине равен: ВОС=АОД-(АОВ+СОД)=180-(60+60)=60 градусов. Тогда углы при основании равны: ОВС=ОСВ=(180-60)/2=60 градусов. Значит, тр-к ВОС - равносторонний, тогда ВС=ВО=СО=R=6 см.
4) Нижнее основание трапеции АД=АО+ОД=6+6=12 см.
5) Р=6+6+6+12=30 см.