Решитеееее срочнооооо

Question

Дан 1 ответ

gartenzie_zn · Answer 1 · 2018-04-14T03:45:33+0000

Ответ на 8-ую задачу 300 минут! Что ввидно на графике.

Задача 9:

$S = vt - \frac{at^2}{2}$ ;

Подставляем значения:

$\frac{1176}{11} = 21t - \frac{21}{22}t^2$ ;

$\frac{21}{22}t^2 - 21t + \frac{1176}{11} = 0 || : 21$

$\frac{t^2}{22} - t + \frac{56}{11} = 0 || \cdot 22$

$t^2 - 2 \cdot 11 \cdot t + 112 = 0$ ;

$D_1 = 11^2-112 = 3^2$ ;

$t_1=11-3 = 8$ мин $= 480$ секунд;

$t_2=11+3 =14$ мин ;

ОБА КОРНЯ ПОЛОЖИТЕЛЬНЫЕ. Второй – показывает возвратное движение автомобиля, поэтому берём первый в секундах, как и требуется по условию.

Ответ: 480 секунд.

*** Некоторые пользователи даже после долгих, подробных и упорных объяснений (вне зависимости от кратких формулировок) так и не могут понять, почему берётся именно первый корень, а второй корень не берётся в расчёт вообще и отбрасывается, как посторонний.

Ничего не остаётся, как всё-таки, подробно разжевать для тех, кто не может понять, эту ситуацию.

Сделаем эквивалентную замену в решении.

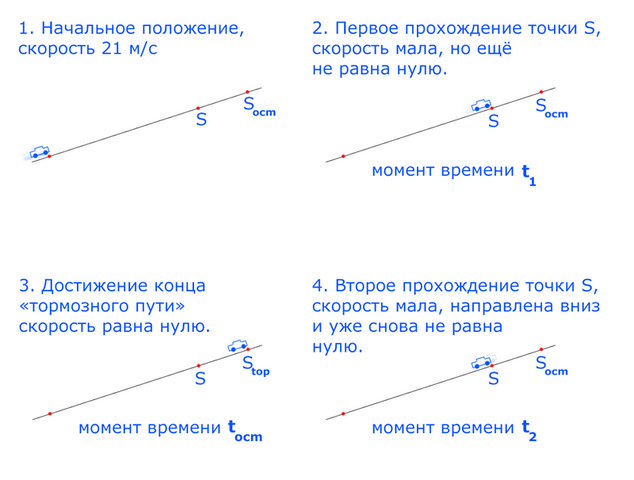
А именно. Вместо использования тормоза в автомобиле, заставим этот автомобиль ТОЧНО на такой же скорости (но уже без использования встроенного тормоза) ехать по поверхности с идеальным сцеплением без проскальзывания с абсолютно твёрдыми колёсами (так чтобы исключить трение качения). При этом эта поверхность будет плоской, но наклонной, так чтобы автомобиль ехал «в горку» и постепенно останавливался из-за гравитации. При этом подберём угол наклона этой горки точно так, чтобы замедление автомобиля, т.е. его отрицательное ускорение, было в точности равно данному в условии, т.е. чтобы было $|a| = \frac{21}{11}$ м/с².

Иллюстрация такого движения показана на рисунке.

Полное время, за которое обратное ускорение доведёт до нуля начальную скорость, можно вычислить по формуле, которая непосредственно следует из самого определения понятия ускорения: $t_{ocm} = v/a = 21 : \frac{21}{11}$ минут $= 11$ минут. Это время, время $t_{ocm}$ – это и есть полное время торможения автомобиля, т.е. до остановки!

При этом можно найти и путь, который проходит автомобиль, т.е. его полный (!) тормозной путь $S_{mop}$ . Для этого можно воспользоваться «безвременнóй» формулой кинематики равноускоренного движения, гласящей, что удвоенной произведение ускорения (в данном случае отрицательного) и пройденного пути равно разности квадратов краевых скоростей, т.е. что:

$2 S_{mop} a = 0 - v^2$ ;

Откуда: $S_{mop} = - \frac{v^2}{2a} = - 21^2 : ( - 2 \cdot \frac{21}{11} )$ м $= 11 \cdot 21 : 2$ м $= 115.5$ м ;

Итак, полный тормозной путь составляет $S_{mop} = 115.5$ м, что больше, чем данное в условии значений пути $S = \frac{1176}{11}$ м $= 106 \frac{10}{11}$ м $\approx 106.9$ м . Т.е., нужно понимать, что нас спрашивают не просто о времени, за которое автомобиль остановится, которое, как уже выяснили, составляет $= 11$ минут, а о времени, за которое автомобиль достигнет некоторой точки (не конечной) на длине тормозного пути, а именно расстояния $\approx 106.9$ м, составляющего только часть (!) от всего тормозного пути $= 115.5$ м.

>>> продолжение текста на изображении >>>