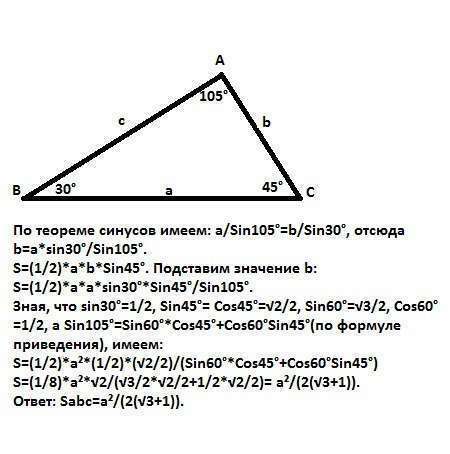
По теореме синусов имеем: a/Sin105°=b/Sin30°, отсюда b=a*sin30°/Sin105°.
S=(1/2)*a*b*Sin45°. Подставим значение b:
S=(1/2)*a*a*sin30°*Sin45°/Sin105°.
Зная, что sin30°=1/2, Sin45°= Cos45°=√2/2, Sin60°=√3/2, Cos60°=1/2, а Sin105°=Sin60°*Cos45°+Cos60°Sin45°(по формуле приведения), имеем:
S=(1/2)*a²*(1/2)*(√2/2)/(Sin60°*Cos45°+Cos60°Sin45°)
S=(1/8)*a²*√2/(√3/2*√2/2+1/2*√2/2)= a²/(2(√3+1)).
Ответ: Sabc=a²/(2(√3+1)).