MB= AB/2
BC/AB=1/2 <=> BC= AB/2 =MB
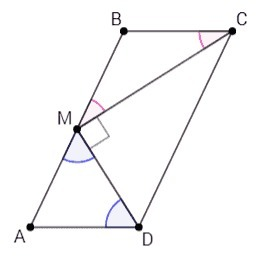
△BMC - равнобедренный.
∠BMC=∠BCM
Аналогично ∠AMD=∠ADM
∠A= 180°-∠AMD-∠ADM =180°-2∠AMD
∠B= 180°-∠BMC-∠BCM =180°-2∠BMC
Cумма односторонних углов при параллельных прямых равна 180°.
∠A+∠B=180° <=>
180° -2∠AMD +180° -2∠BMC =180° <=>
∠AMD+∠BMC =180°/2 =90°
∠CMD= 180°-∠AMD+∠BMC =180°-90° =90°
ИЛИ
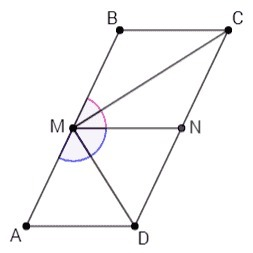
Средняя линия MN делит ABCD на два равных параллелограмма. Основания ABCD равны половинам его сторон, следовательно BMNC и AMND - ромбы. Диагонали ромба являются биссектрисами его углов.
∠CMD =∠CMN+∠DMN =∠BMN/2+∠AMN/2 =180/2 =90.