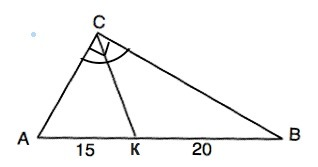
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
В треугольнике АВС, где СК - биссектриса, АС:ВС=АК:ВК=15/20=3/4
Примем коэффициент отношения катетов равным х.
Тогда АС=3х, ВС=4х
По т.Пифагора АВ²=АС²+ВС²
35²=9х²+16х²
7²•5²=25х²⇒
х²=7²
х=7 см
АС=3х=21 см
ВС=4х=28 см