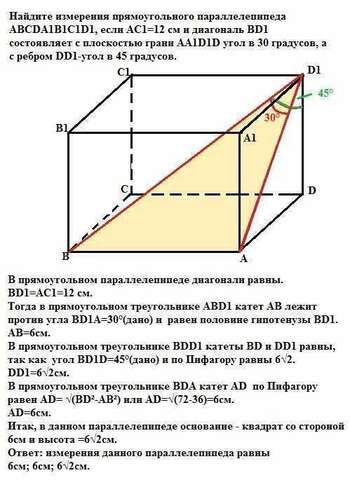
В прямоугольном параллелепипеде диагонали равны.
BD1=AC1=12 см.
Тогда в прямоугольном треугольнике АВD1 катет АВ лежит против угла BD1A=30°(дано) и равен половине гипотенузы BD1.
АВ=6см.
В прямоугольном треугольнике BDD1 катеты BD и DD1 равны, так как угол BD1D=45°(дано) и по Пифагору равны 6√2.
DD1=6√2см.
В прямоугольном треугольнике BDА катет АD по Пифагору равен AD= √(BD²-АВ²) или AD=√(72-36)=6см.
АD=6см.
Итак, в данном параллелепипеде основание - квадрат со стороной 6см и высота =6√2см.
Ответ: измерения данного параллелепипеда равны
6см; 6см; 6√2см.