1) в треугольнике ABC высоты AK и BE пересекаются в точке O . угол CAB = 42градусов ....

Question

1) в треугольнике ABC высоты AK и BE пересекаются в точке O . угол CAB = 42градусов . чему равен угол ABE 2) В равнобедренном треугольнике ABC AB=BC , медианы AE и CK пересекаются в точке M . BM=6 см, AC=10 см . Найти площадь треугольника ABC

Answer 1

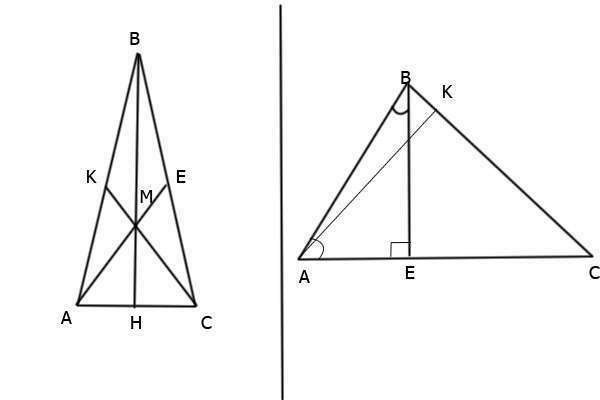
Так как ВЕ - высота, то угол ВЕА = 90 градусов. Получается треугольник АВЕ. Угол АВЕ = 180 - 42 - 90 = 48.

Медианы точкой пересечения делятся в отношении 2:1 считая от вершины. Поэтому 6 см - 2 части, 1 часть - 3 см. ВН = 9 см. Площадь треугольника находим:

S = = 45 см^2

---