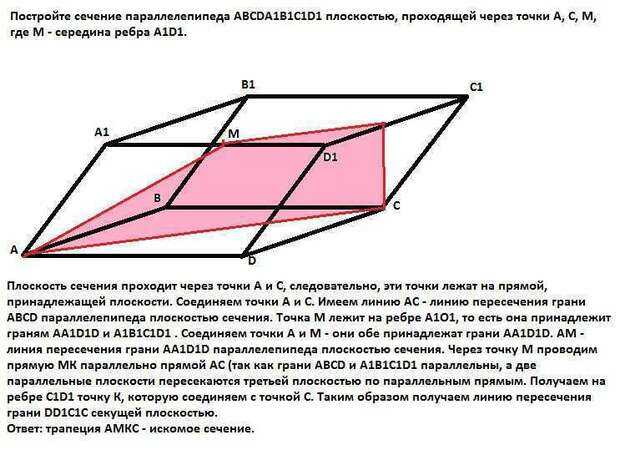
Плоскость сечения проходит через точки А и С, следовательно, эти точки лежат на прямой, принадлежащей плоскости. Соединяем точки А и С. Имеем линию АС - линию пересечения грани АВСD параллелепипеда плоскостью сечения. Точка М лежит на ребре А1О1, то есть она принадлежит граням АА1D1D и А1В1С1D1 . Соединяем точки А и М - они обе принадлежат грани АА1D1D. АМ - линия пересечения грани AA1D1D параллелепипеда плоскостью сечения. Через точку М проводим прямую МК параллельно прямой АС (так как грани АВСD и A1B1C1D1
параллельны, а две параллельные плоскости пересекаются третьей плоскостью по параллельным прямым. Получаем на ребре С1D1 точку К, которую соединяем с точкой С. Таким образом получаем линию пересечения грани DD1C1C секущей плоскостью.
Ответ: трапеция АМКС - искомое сечение.