Решаем 2 уравнения:
x+1=0; x-2=0
x=-1 ; x=2
У нас получилось 2 точки х: -1 и 2. Нужно отметить их на графике. Таким образом мы получили 3 области:
минус бесконечность, -1 ;
-1, 2
2, плюс бесконечность.
Далее мы раскрываем модули для первой области
обе функции: x+1 и x-2 на этом отрезке принимают отрицательные значения. Значит, мы раскрываем модуль по правилу |f(x)| = -f(x)
y= -(x+1)-(x-2) = -x-1-x+2 = -2x+1
Далее раскрываем модули на интервале от -1 до 2
x+1 >=0
x-2 <=0<br>y = x+1-x+2 = 3
И раскрываем модули на интервале от 2 до плюс бесконечность
бе функции: x+1 и x-2 на этом отрезке принимают положительные значения. Значит, мы раскрываем модуль по правилу |f(x)| = f(x)
y = x+1 + x-2 = 2x-1
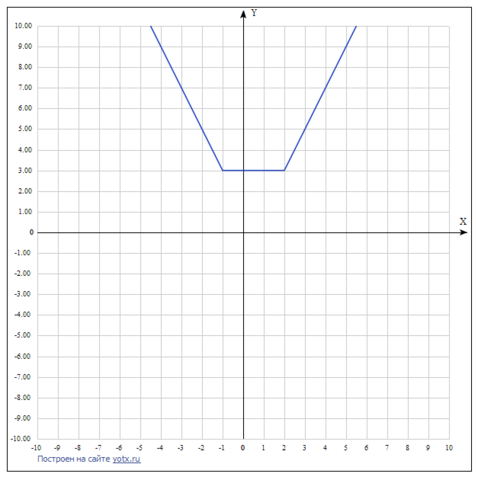
В итоге получаем 3 функции на разных интервалах:
1) y = -2x+1
2) y = 3;
3) y = 2x+1
Строим график функции