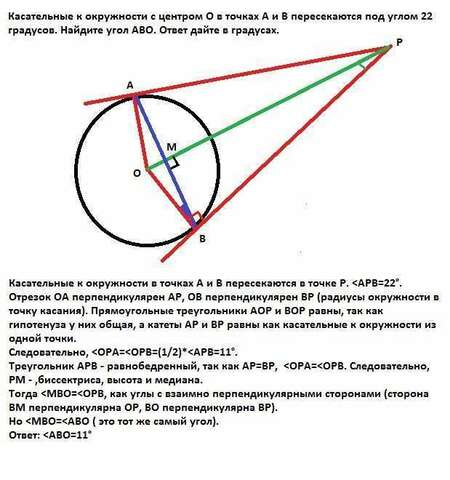
Касательные к окружности в точках А и В пересекаются в точке Р. Отрезок ОА перпендикулярен АР, ОВ перпендикулярен ВР (радиусы окружности в точку касания). Прямоугольные треугольники АОР и ВОР равны, так как гипотенуза у них общая, а катеты АР и ВР равны как касательные к окружности из одной точки.
Следовательно, <ОPА=<ОPВ=(1/2)*<APB=11°.<br>Треугольник АРВ - равнобедренный, так как АР=ВР, <ОPА=<ОPВ. Следовательно, РМ - ,биссектриса, высота и медиана.<br>Тогда Но Ответ: