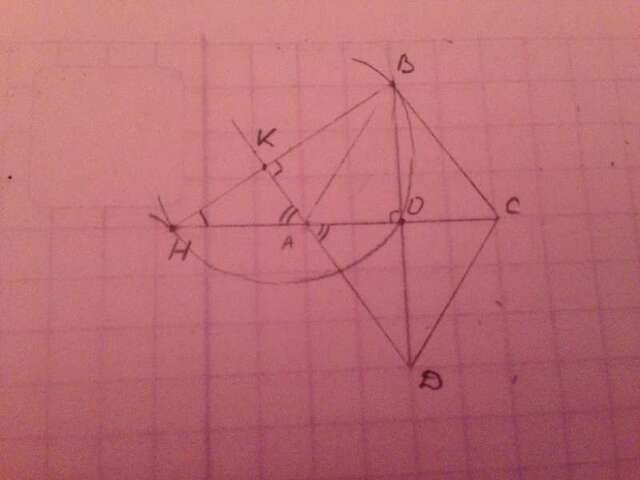Высота ВК к стороне АД, пересекает прямую с АС в точке Н. Косинус угла ВНО равен 0,8.
ΔНОВ - прямоугольный (<НОВ- прямой, т.к. диагонали ромба перпендикулярны). Центром описанной около прямоугольного треугольника окружности является середина гипотенузы<span>. Значит НВ=2R=2*2.5=5.
НО=НВ*соsВО=√HB²-HO²=√25-16=√9=3
Тогда диагональ ромба ВД=2ВО=6 (диагонали ромба в точке пересечения делятся пополам ВО=ОД, АО=ОС))
Рассмотрим прямоугольные ΔНКА и ΔДОА: у них <НАК=<ДАО (вертикальные), <НКА=<ДОА=90°, значит эти треугольники подобны по 1 признаку.<br>НА/АД=НК/ОД=КА/АО
Из ΔНКА НК=НА*соsПодставляем:
НА/АД=0,8НА/3
АД=3/0,8=3,75
АО=√(АД²-ОД²)=√(3,75²-3²)=√5,0625=2,25
АС=2АО=2*2,25=4,5
Площадь ромба S=АC*ВД/2
2S=АС*ВД=4,5*6=27
Ответ: 27