Рассмотрим область |x| + |y| <= 1 и прямую Ax + By = 1. Даны числа A и B.Если область и...

Question

Дан 1 ответ

Правильный ответ

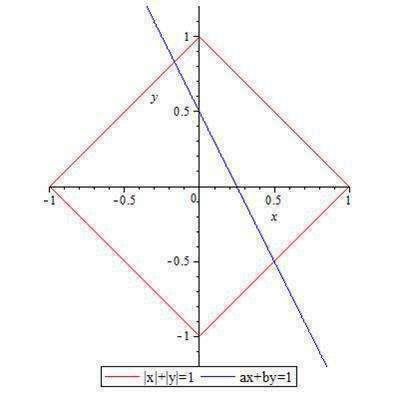
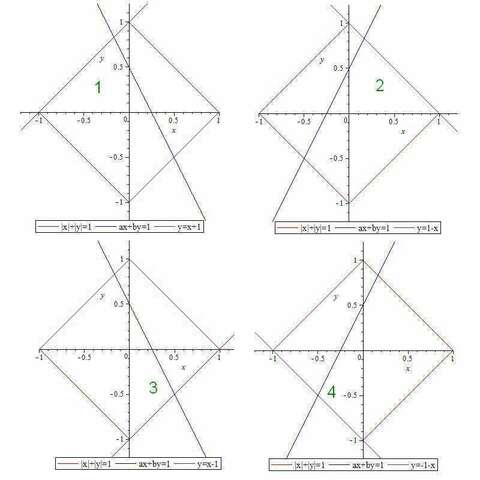
График функции |x|+|y|=1 - это квадрат с вершинами в точках (-1;0), (0;1), (1;0) и (-1;-1), следовательно описываемая область является квадратом, включая его границы (вложение 1). Прямая Ax+By=1 (далее - просто прямая) может иметь с областью одну общую точку в случае, если она проходит через одну из вершин квадрата. Также, она может не иметь общих точек, либо иметь их бесконечное множество на отрезке, параллельном одной из сторон квадрата или пересекающим этот квадрат. Рассмотрим по очереди случаи пересечения (включая касание) прямой с каждой из сторон квадрата (вложение 2).
Чтобы определить координаты точки пересечения двух прямых, нужно совместно решить систему двух уравнений.

Вариант 1. Уравнение линии y=x+1

$\begin {cases} y=x+1 \\ Ax+By=1\end {cases} \to \quad \begin {cases} y=x+1 \\ \displaystyle y= \frac{1}{B} (1-Ax) \end {cases} \\ \displaystyle \frac{1}{B} (1-Ax)=x+1; \ 1-Ax=Bx+B, \ B\ne 0 \\ x= \frac{1-B}{A+B}; \ A+B \ne 0$
Для того, чтобы точка пересечения лежала на рассматриваемой стороне квадрата, для найденного значения х должно выполняться условие x∈[-1;0]
Cделанные при получении выражения для х ограничения рассмотрим позднее.

Вариант 2. Уравнение линии y=1-x

$\begin {cases} y=1-x \\ Ax+By=1\end {cases} \to \quad \begin {cases} y=1-x \\ \displaystyle y= \frac{1}{B} (1-Ax) \end {cases} \\ \displaystyle \frac{1}{B} (1-Ax)=1-x; \ 1-Ax=-Bx+B, \ B\ne 0 \\ x= \frac{B-1}{B-A}; \ B \ne A$
Для того, чтобы точка пересечения лежала на рассматриваемой стороне квадрата, для найденного значения х должно выполняться условие x∈[0;1]

Вариант 3. Уравнение линии y=x-1

$\begin {cases} y=x-1 \\ Ax+By=1\end {cases} \to \quad \begin {cases} y=x-1 \\ \displaystyle y= \frac{1}{B} (1-Ax) \end {cases} \\ \displaystyle \frac{1}{B} (1-Ax)=x-1; \ 1-Ax=Bx-B, \ B\ne 0 \\ x= \frac{1+B}{A+B}; \ A+B \ne 0$

Для того, чтобы точка пересечения лежала на рассматриваемой стороне квадрата, для найденного значения х должно выполняться условие x∈[0;1]

Вариант 4. Уравнение линии y=-x-1

$\begin {cases} y=-x-1 \\ Ax+By=1\end {cases} \to \quad \begin {cases} y=-x-1 \\ \displaystyle y= \frac{1}{B} (1-Ax) \end {cases} \\ \displaystyle \frac{1}{B} (1-Ax)=-x-1; \ 1-Ax=-Bx-B, \ B\ne 0 \\ x= \frac{1+B}{A-B}; \ A \ne B$
Для того, чтобы точка пересечения лежала на рассматриваемой стороне квадрата, для найденного значения х должно выполняться условие x∈[-1;0]
Объединенное условие:
$\begin {cases} \displaystyle \left( x= \frac{1-B}{A+B}\right) \lor \left( x= \frac{1+B}{A-B} \right) , \ x\in[-1;0] \\ \displaystyle \left( x= \frac{B+1}{B+A}\right) \lor \left( x= \frac{B-1}{B-A} \right) , \ x\in[0;1] \end {cases}$
Ограничения на коэффициенты A и B
Очевидно, что одновременно оба коэффициента не должны быть нулевыми.
Если А=0, то получаем уравнение By=1 или y=1/B. Этому уравнению соответствуют линии, располагающиеся параллельно оси OX. Очевидно, что нам подходят значения в интервале [-1;1], откуда получаем |B|≥1.
Для B=0 получаем уравнение Ax=1 или x=1/A и по аналогии |A|≥1.
При A=B уравнение прямой приобретает вид Ax+Ay=1 или y=1/A+x. Это прямые, параллельные сторонам квадрата в вариантах 1 и 3. Нас устроит, если х∈[-1..1] и такой интервал совпадает с определенным нами в объединенном условии. Для этого |A|≥1
При A+B=0 уравнение прямой приобретает вид Ax-Ay=1 или y=1/A-x. Это прямые, параллельные сторонам квадрата в вариантах 2 и 4. Нас снова устроит, если х∈[-1..1] и снова такой интервал совпадает с определенным нами в объединенном условии. А для этого случая |A|≥1.
Сделанный анализ позволяет составить программу (версия PascalABC.Net)

var
a,b:real;
begin
Writeln('Принадлежность хотя бы одной точки прямой к области');
Write('Укажите коэффициенты A и B уравнения Ax+By=1: ');
Read(a,b);
if (a=0) and (b=0) then Writeln('Решения нет')
else
    if a=0 then
      if abs(b)>=1 then Writeln('Точка пересечения есть')
      else Writeln('Точки пересечения нет')
    else
      if (b=0) or (a=b) or (a=-b) then
        if abs(a)>=1 then Writeln('Точка пересечения есть')
        else Writeln('Точки пересечения нет')
      else
        if (((1-b)/(a+b))>=-1) and (((1-b)/(a+b))<=0) or <br>          (((1+b)/(a-b))>=-1) and (((1+b)/(a-b))<=0) <br>          then Writeln('Точка пересечения есть')
        else
          if (((b+1)/(b+a))>=0) and (((b+1)/(b+a))<=1) or <br>          (((b-1)/(b-a))>=0) and (((b-1)/(b-a))<=1) <br>          then Writeln('Точка пересечения есть')
          else Writeln('Точки пересечения нет')
end.

Alviko_zn (142k баллов) 03 Апр, 18