Условие №1 неполное.
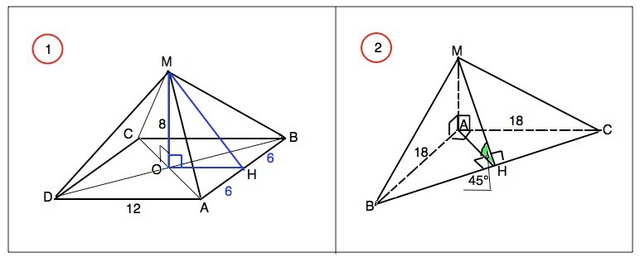
№2. Высота правильной четырехугольной пирамиды равна 8 см, сторона ее основания 12 см. Вычислите длину бокового ребра пирамиды и площадь боковой поверхности пирамиды.
---------
В основании пирамиды квадрат, она правильная - значит, основание ее высоты находится в точке пересечения диагоналей квадрата, а все грани - равные равнобедренные треугольники.
Ребро МD=√(ОD²+ОМ²)
ОМ=8 см, ОD - половина диагонали квадрата и равно 6√2
МD=√(72+64)=√136=4√34 - это длина бокового ребра.
Площадь боковой поверхности равна произведению апофемы ( высоты боковой грани)
на половину периметра основания.
S=MH•4•АD:2=
МН•2АD
МН из треугольника МОН ( египетского!) равно 10 ( можно проверить по т. Пифагора)
S(бок)=10•24=240 см²
----------------
№3
Ребро МА пирамиды МАВС перпендикулярно плоскости ее основания АВ=АС=18 см , угол ВАС=90 градусов. Угол между плоскостями основания и гранью МВС равен 45 градусов. Вычислите: