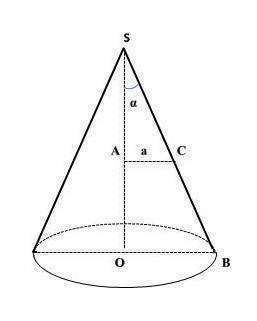
Рассмотрим прямоугольный ΔОSB, в котором катет SО (высота конуса), катет ОВ (радиус основания конуса), гипотенуза SВ (образующая конуса).
По условию угол между образующей и высотой равняется α, т.е. Середина образующей (точка С) удалена от оси ОS на расстояние а, это значит АС=а, SС=СВ и АС перпендикулярно SО и параллельно ОВ.
Исходя из т.Фалеса (если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой стороне) SА=АО, а это значит, что АС является средней линией ΔОSВ (она соединяет середины двух данных сторон, параллельна третьей стороне и равна ее половине), тогда ОВ=2АС=2a.
SB=OB/sin α=2a/sin α
SO= SB*cos α=2a*cos α/sin α=2а*сtg α
Объем конуса V= π*R²*H/3=π*ОВ²*SO/3=π*4a²*2a*ctg α/3=8a³*ctg α/3