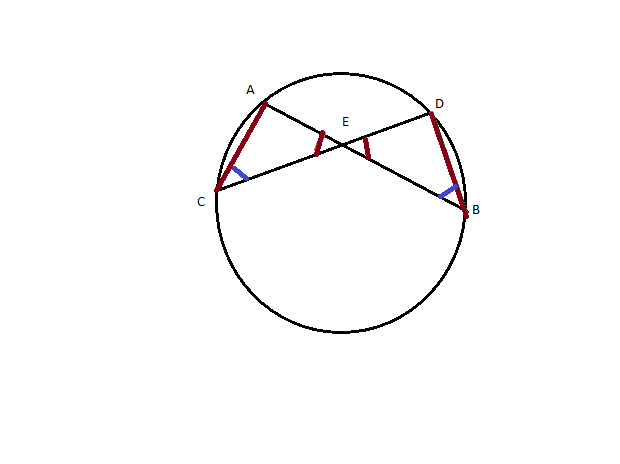
При пересечении двух хорд, произведения значений длин отрезков, образованных точками пересечения и концами хорд, равны.
Док-во:
Угол АСЕ = Угол ABD, как углы, опирающиеся на одну дугу в окружности.
Угол AEC=Угол BED, как вертикальные. След-но треугольник AEC подобен треугольнику DBE. Из подобия треугольников следует:
AE/EC = ED/BE --> AE*BE = EC*ED, что и требовалось док-ть.