Квадрат АВСD и АВС1D1 лежат в плоскостях, угол между которыми равен 60 градусов. Найдите...

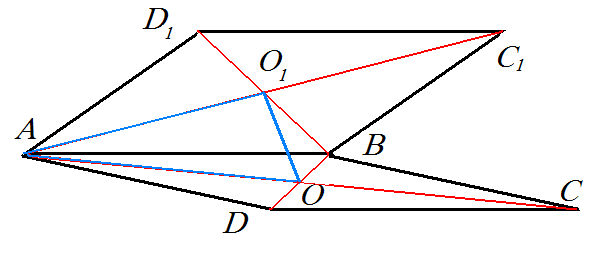
Дано:
квадрат ABCD = квадрат ABC₁D₁
AB = a
AC = AC₁ = d
угол DAD₁ = угол CAC₁ = 60°
Найти: OO₁

Решение:
По формуле диагонали квадрата
$d = AC=a \sqrt{2}$ ⇒
⇒ AO = AO₁ = $\frac{1}{2} * a\sqrt{2}$ = $\frac{ \sqrt{2} }{2} *a = \frac{1}{2}a$ ⇒
⇒ ΔO₁AO - равнобедренный
Так как угол O₁AO = 60°, а по сумме углов 180 - 60 = 120°, то другие два угла OO₁A = O₁OA = 120/2 = 60°. Следовательно ΔO₁AO - равносторонний O₁A = AO = OO₁ = $\frac{1}{2}a$
Ответ: расстояние между центрами равно $\frac{1}{2}a$