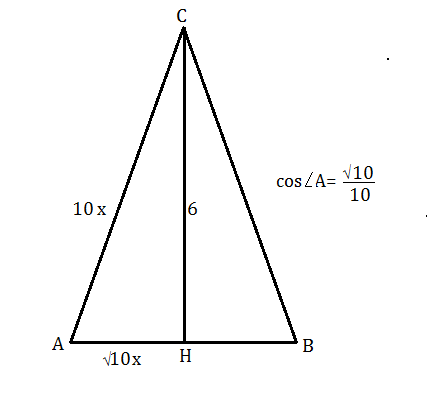АС=ВС, ⇒ ∆ АВС - равнобедренный, и высота СН является его медианой. АН=ВН
АВ=2АН
Синус угла - это отношение катета, прилежащего к данному углу, к гипотенузе.
Пусть коэффициент отношения АН:АС будет
х.
Тогда АС=10х, АН=√10 хТ
.к. СН - высота, ∆ АСН - прямоугольный.
По т.Пифагора
СН²=АС²-АН²
36=100х² - 10х²
10х²=4
х²=4/10
х=2/√10⇒
АН=(√10)* 2√10=2
АВ=2АН=4