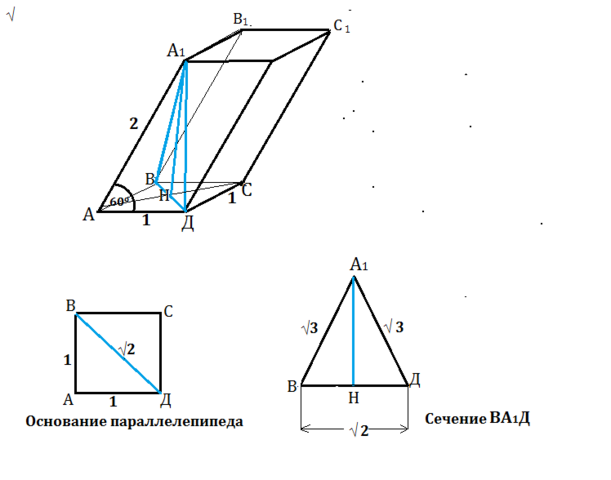
Основание параллелепипеда - квадрат, сторона которого равна 1м. Одно из боковых ребер равно 2 м и образует с каждой из прилежащих сторон основания угол 60º. Найдите объем параллелепипеда.
---------------
Из условия ясно, что данный параллелепипед -
наклонный, т.к. ребро
не перпендикулярно основанию.
Объем параллелепипеда равен произведению его высоты на площадь основания.
V=S*h
Т.к. основание - квадрат, площадь его равна квадрату стороны.
S=а²=1 м²
Высоту параллелепипеда нужно найти.
Сделаем рисунок.
Ребро АА₁ образует со прилежащими сторонами основания АВ и АД углы А₁АВ и А₁
АД, равные 60°. Опустим из А₁ перпендикуляры на стороны АВ и АД.
В прямоугольном треугольнике с острым углом 60º второй острый угол равен 30º , противолежащий ему катет равен половине гипотенузы. Здесь он равен А₁А
:2=1.
Т.к. стороны основания равны 1, АВ и АД - катеты получившихся прямоугольных треугольников.
Треугольники А₁
АД и А₁
АВ равны по равному катету, острому углу и общей гипотенузе. ⇒
А₁В=А₁Д
Соединим В и Д. В треугольнике ВА₁Д
А₁В=А₁Д и являются боковыми сторонами равнобедренного треугольника ВА₁Д.
А₁Д=АА₁*sin (60º)=(2√3)/2=√3 м ( можно найти и по т.Пифагора)
Высота параллелепипеда - перпендикуляр А₁Н, опущенный из А₁ на основание. В то же время А₁Н - высота равнобедренного треугольника ВА₁Д.
Так как основание параллелепипеда - квадрат, ВД - его диагональ и по свойству диагонали квадрата
ВД=АВ*√2=1*√2=√2.
В треугольнике ВА₁
Д половина ВН диагонали равна ВД:2=(√2):2
По т.Пифагора
А₁Н²=А₁В² - НВ²
А₁Н=√(3-2/4)=√2,5=√(25/10)=5/√10=0,5√10 м
V=S( АВСД)*h=1*0,5√10=0,5√10 м³