Боковое ребро правильной четырехугольной пирамиды,равное12см,образует с плоскостью...

Question

Дан 1 ответ

Правильный ответ

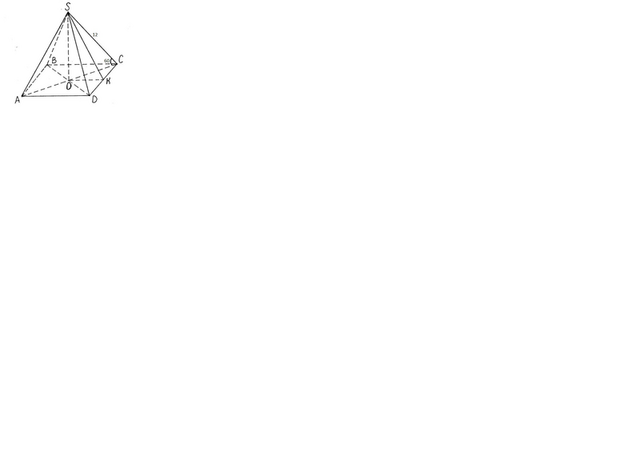
$SABCD -$ правильная четырехугольная пирамида

$SO =H -$ высота пирамиды

$SK=l-$ апофема

$SC=12$ см

$\ \textless \ SCO=60^\circ$

Так как $SABCD$ - правильная четырехугольная пирамида, значит в основании лежит квадрат, т.е. $ABCD$

$AC$ ∩ $BD=O$

$V_{n} = \frac{1}{3} S_{ocn}*H$

$S_{bok}= \frac{1}{2} P_{ocn}*l$

$SO$ ⊥ $(ABC)$ , значит Δ $SOC-$ прямоугольный

$\frac{SO}{SC} =sin 60^\circ$

$SO=SC*sin60^\circ =12* \frac{ \sqrt{3} }{2} =6 \sqrt{3}$ см

$\frac{OC}{SC} =cos60^\circ$

$OC=SC*cos60^\circ =12* \frac{1}{2} =6$ см

$AC=2OC=2*6=12$ см

$AC=d$ - диагональ квадрата

$d=a \sqrt{2}$

$a \sqrt{2} =12$

$a= \frac{12}{ \sqrt{2} } = \frac{12 \sqrt{2} }{2} =6 \sqrt{2}$ см, где $a$ - сторона квадрата

$S_{ocn}=a^2=(6 \sqrt{2} )^2=36*2=72$ см²

$V_{n}= \frac{1}{3} *72*6 \sqrt{3} =144 \sqrt{3}$ см³

$P_{ocn}=4a=4*6 \sqrt{2}=24 \sqrt{2}$ см

$OK= \frac{1}{2} AD= \frac{1}{2}*6 \sqrt{2} =3 \sqrt{2}$ см

Δ $SOK$ - прямоугольный

по теореме Пифагора найдём

$SK= \sqrt{SO^2+OK^2}= \sqrt{(6 \sqrt{3})^2+(3 \sqrt{2} )^2 } = \sqrt{108+18}= \sqrt{126}=$ $3 \sqrt{14}$ см

$S_{bok}= \frac{1}{2}*24 \sqrt{2} *3 \sqrt{14}=36 \sqrt{28}=36*2 \sqrt{7} =72 \sqrt{7}$ см²

Ответ: $72 \sqrt{7}$ см² ; $144 \sqrt{3}$ см³

mukus13_zn (83.6k баллов) 02 Апр, 18