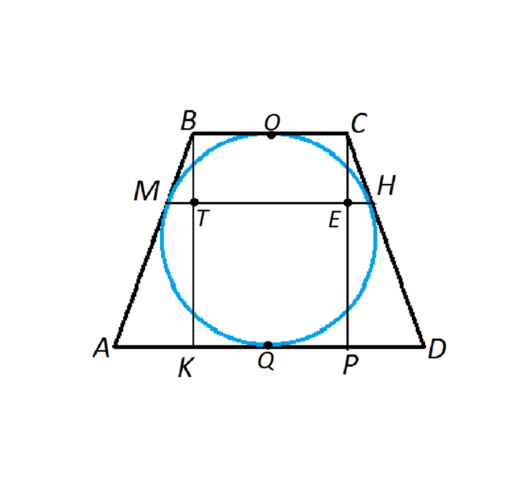
В четырехугольник, значит, и в трапецию, вписать окружность можно тогда и только тогда, когда суммы ее противоположных сторон равны.
Следовательно,
АВ+СD=AD+BC=20
В комментарии к условию указано, что
трапеция равнобедренная. Следовательно.
АВ=СD=20:2=
10
Соединим точки касания окружности М и Н.
Опустим из В и С перпендикуляры ВК и СР.
КР=ВС=
ТЕ=
6
АК=(АD-DC):2=(14-6):2=
4
По свойству отрезков касательной из одной точки
ВМ=ВО=ОС=СН=
3
Тогда
АМ=НD=10-3=
7
Рассмотрим треугольники АВК и ВМТ.
Они подобны, т.к. МН параллельна АD⇒.
МТ:АК=ВМ:ВА
МТ:4=3:10
10 МТ=12
МТ=1,2
ЕН=МТ
МН=МТ+ТЕ+ЕН=8,6