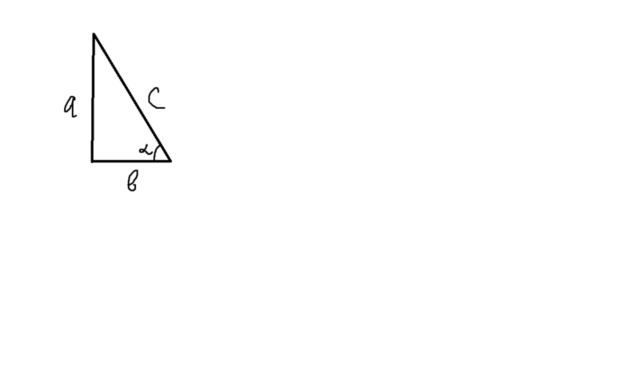Тут можно поступить таким образом. Пусть arccos 2/√5 = α. Тогда по определению арккосинуса cos α = 2/√5. Из нашего выражения понятно, что нам надо найти sin α. Поступим для этого так. Рассмотрим прямоугольный треугольник, пусть угол α будет там, где указано на рисунке. Мы знаем, косинусом данного угла является отношение
b/c. Отсюда получаем, что b = 2, c = √5.
sin α = a/c. Найдём a по теореме Пифагора:
a = √(c²-b²) = √5-4 = √1 = 1
sin α = a/c = 1 / √5 = √5 / 5
Поскольку arccos 2/√5 = α, то синус данного угла - это то, что мы искали, то есть sin(arccos 2/корень 5) = √5/5. Задача выполнена.