У=1/3 х^3-x^2+1
y'= x^2 - 2x
x^2 - 2x = 0
x (x-2)=0
x=0 или x=2
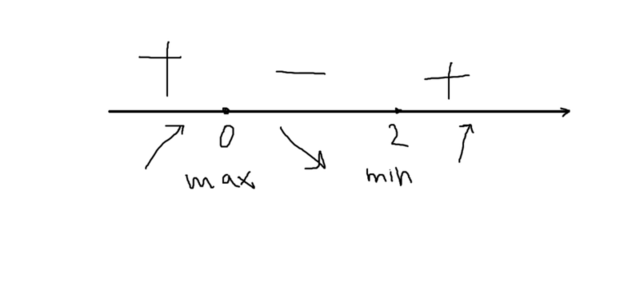
0 и 2 принадлежат промежутку (-1,3), определим знаки производной
См. вложение
Найдем значения функции
y(-1) = -1/3 - 1+1 = -1/3 - минимальное
y(0) = 1 - максимальное
y(2) = 1/3 * 8 - 4 + 1 = 8/3 - 4 -1 = 8-12 / 3 +3/3 = -1/3 - минимальное
y(3) = 1/3 * 27 - 9 +1 = 1 - максимальное