Я еще ничего не сделал, а меня уже благодарят :( придется выложить решение. Я тогда сделаю такое решение, которое имеет самостоятельную методическую ценность. К тому же это и наиболее логичный метод решения. Курсив, как всегда, можно не читать.
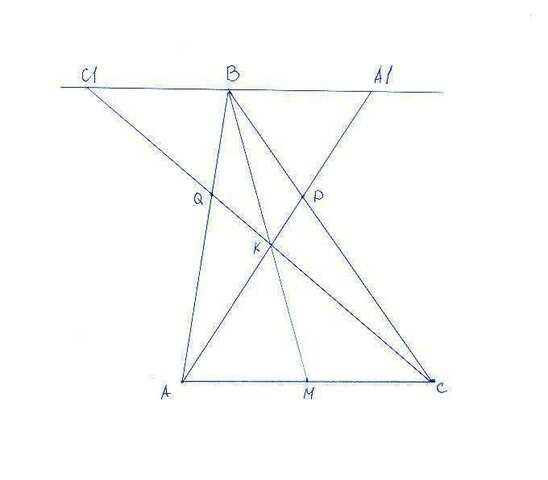
Пусть через вершину B проведена прямая параллельно AC;
AK (или, то же самое - AP) пересекает эту прямую в точке A1; CK пересекает BA в точке Q и BA1 - в точке C1;
Треугольники BPA1 и APC подобны, поэтому BA1/AC = BP/PC;
Треугольники BKA1 и AKM подобны, поэтому BA1/AM = BK/KM;
То есть BP/PC = BA1/AC = (1/2)*BA1/AM = (1/2)*BK/KM;
Точно также показывается, что BQ/QA = (1/2)*BK/KM = BP/PC; Это означает, что QP II AC; и это - НЕ ЗАВИСИТ от того, где именно на медиане BM расположена точка K (условие BK/KM = 10/9; пока не использовалось).Это - очень важный результат сам по себе.
Таким образом, BP/PC = 5/9;
Дальше слова "площадь треугольника ABC" будут записываться, как Sabc;
Sbmc = Sabc/2 = S/2;
Skmc = Sbmc*KM/BM = (S/2)*9/(9 + 10) = (S/2)*(9/19);
Sbkc = (S/2)*(10/19);
Spkc = Sbkc*PC/BC = Sbkc*9/(9 + 5) = (S/2)*(10/19)*(9/14);
Smkpc = Smkc + Spkc = (S/2)*(9/19)*(1 + 10/14) = S*(9/19)*(6/7) = S*54/133;
Smkpc/Sabc = 54/133;