1)Чтобы доказать подобие треугольников А1С1В и АВС , надо начинать не с них, а с треугольников АА1В и СС1В. Вот они точно подобны по 2 угла( они прямоугольные и углы при точке В вертикальные)
а это значит, что в этих треугольниках стороны пропорциональны,
т.е. А1В/ВС1 = АВ/ ВС. А эти стороны являются сторонами и искомых треугольников. Получается, что ΔАВС подобенΔА1ВС1 по 2 признаку ( 2 стороны одного треугольника пропорциональны двум сторонам другого и углы между ними равны) А углы между ними при точке В вертикальные.
2) Здесь надо рассматривать подобные треугольники. А отношение подобных треугольников = квадрату коэффициента подобия. Так что площади относятся как 1:9
3)Надо разобраться с модулем. Если есть в записи модуль, то это означает, что у тебя не одна запись, а две, но уже без знака модуля. Говорят: снять знак модуля. Вот давай, будем снимать. При этом учтём. что
|x| = x при х ≥ 0 (*)
|x| = - x при х меньше 0 (**)
а) (х² -9)/3х ≥ 0
Решим это неравенство методом интервалов
х² - 9 = 0 ⇒ х = +-3
3х = 0 ⇒ х = 0
-∞ -3 IIIIIIIIII 0 3 IIIIIIIIIIII +∞
+ - - + это знаки (х² - 9)
- - + + это знаки 3х
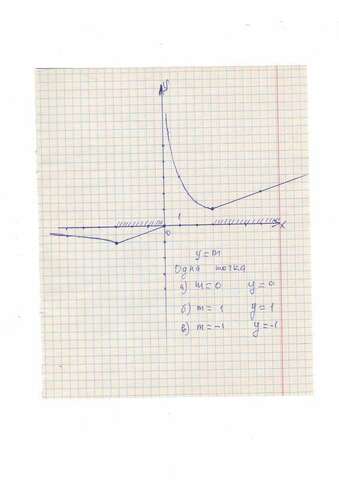
Получилось 2 промежутка, на которых надо строить график (вернее, куски) функции у = 1/2(х/3 - 3/х + х/3 +3/х) = 1/2·2х/3= х/3. (Учли(*))
у = х/3 - это прямая, которую можно построить по 2 точкам и оставить куски этой прямой на тех промежутках, которые заштрихованы.
б) (х² -9)/3х меньше 0
Решим это неравенство методом интервалов
х² - 9 = 0 ⇒ х = +-3
3х = 0 ⇒ х = 0
-∞IIIIIIIII-3 0 IIIIIIIIIII3 +∞
+ - - + это знаки (х² - 9)
- - + + это знаки 3х
Получилось 2 промежутка, на которых надо строить график (вернее, куски графика ) функции у = 1/2( -х/3 + 3/х + х/3 +3/х) = 1/2·6/х = 3/х. (Учли(**))
у =3/х - это гипербола, расположенная в 1 и 3 четвертях. Её построим по точкам и оставим те куски, которые попадут на наши заштрихованные промежутки.
Теперь можно говорить и о значении m