1) Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и вторую. Предположим, что эта прямая, перпендикулярная первой плоскости, НЕ перпендикулярна второй плоскости. Значит, через точку пересечения прямой и второй плоскости можно провести третью плоскость, перпендикулярную данной прямой и эта третья плоскость будет параллельна первой плоскости, так как обе перпендикулярны одной и той же прямой.
Итак, мы провели через одну точку две плоскости, параллельных первой плоскости, что НЕВОЗМОЖНО.
Следовательно,прямая перпендикулярна второй плоскости.
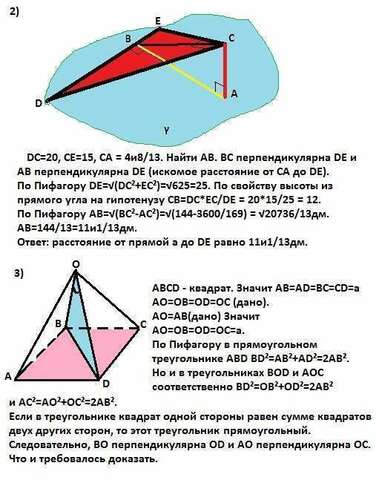
2) DC=20, CE=15, CA = 4и8/13. Найти АВ. ВС перпендикулярна DE и АВ перпендикулярна DE (искомое расстояние от СА до DE).
По Пифагору DE=√(DC²+EC²)=√625=25. По свойству высоты из прямого угла на гипотенузу СВ=DC*EC/DE = 20*15/25 = 12дм.
По Пифагору АВ=√(ВC²-АC²)=√(144-3600/169) = √20736/13дм.
АВ=144/13=11и1/13дм.
Ответ: расстояние от прямой а до DE равно 11и1/13дм.
3)АВСD - квадрат. Значит АВ=АD=ВС=СD=a
АО=ОВ=OD=OC (дано).
АО=АВ(дано) Значит АО=ОВ=OD=OC=а.
По Пифагору в прямоугольном треугольнике АВD ВD²=АВ²+АD²=2АВ².
Но и в треугольниках ВОD и АОС соответственно ВD²=ОВ²+ОD²=2АВ² и АС²=АО²+ОС²=2АВ².
Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то этот треугольник прямоугольный. (Теорема, обратная теореме Пифагора) То есть Следовательно, прямые АО и ОС, а также ВО и ОD перпендикулярны.
Что и требовалось доказать.