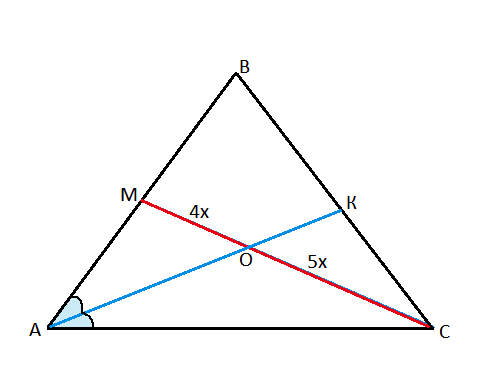
Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
В треугольнике АСМ биссектриса делит медиану на отрезки СО:ОМ=5:4 или МО:ОС=4:5, что одно и то же.
Следовательно, АМ:АС=4:5
Пусть коэффициент отношения сторон треугольника равен х.Тогда
АМ=4х, АС=5х.
СМ - медиана, АВ=АМ+МВ=4х+4х=8х
Отсюда АВ:АС=8х:5х=8:5