Если я правильно поняла, что именно нужно найти.
-------------------------------------------------------------------------------------
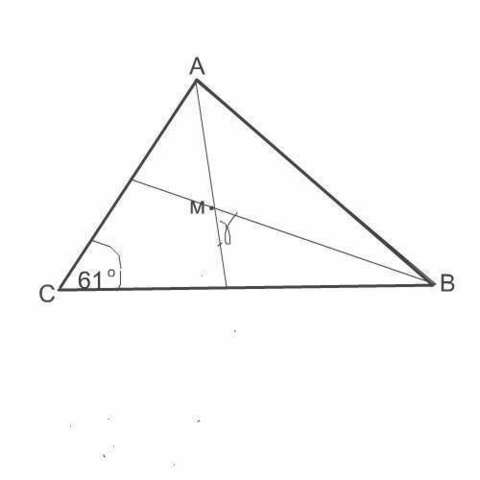
Сделаем к задаче рисунок.
Обозначим точку пересечения биссектрис Δ АВС ( в котором ∠ С равен 61°) буквой М.
Рассмотрим треугольник АВМ.
∠ МАВ = ½ ∠ ВАС,
∠ АВМ = ½ ∠ АВС, тогда ∠ АМВ =180° -½ (∠ АВС + ∠ ВАС).
Острый угол между биссектрисами на рисунке обозначен ɣ.
Угол ɣ смежный с углом АМВ, следовательно, ɣ = ½ (∠ АВС + ∠ ВАС).
Поскольку ∠С треугольника АВС =61°, то ∠ АВС + ∠ ВАС = 119°.
Тогда ɣ =½ (∠ АВС + ∠ ВАС) = 119° : 2 = 59,5°
Ответ: 59,5°
------------
Вариант решения.
Сумма углов ВАС+АВС равна внешнему углу при ВСА ( по теореме о внешнем угле треугольника)
(∠САВ+∠АВС)=180°-61°=119°
Тогда их полусумма равна
119°:2=59,5°
Искомый угол - это угол гамма на приложенном рисунке.
Он является внешним углом при вершине М треугольника ВМА и равен сумме углов, не смежных с углом АМВ. Т.е. угол γ равен полусумме углов ВАМ и АВМ .
Острый угол,образованный между сторонами и биссектрисами его остальных углов
=59,5°