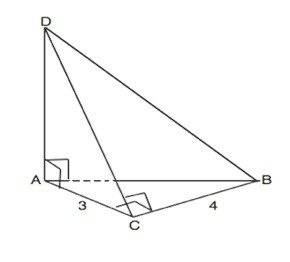
Дано: АD⊥АС, АD ⊥АВ. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Следовательно, АD перпендиулярна плоскости АВС.
Если прямая перпендикулярна к плоскости, то она перпендикулярна к любой прямой, лежащей в этой плоскости.⇒
АD⊥ВС
Наклонная DС⊥ВС по условию, АС - проекция DС на плоскость АВС. По т. о 3-х перпендикулярах АС⊥ВС, и ∆ АВС прямоугольный с прямым углом АСВ.
ВС⊥DC ( дано), ВС⊥АС ( найдено). ⇒ ВС перпендикулярна двум пересекающимся прямым в плоскости ADC, следовательно, ВС перпендикулярна плоскости АDC.
Площадь прямоугольного ∆ АВС=АС•ВС:2=3•4:2=6 (ед. площади)