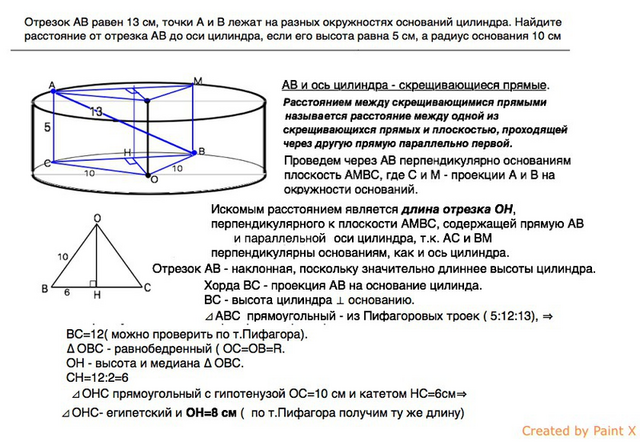
Отрезок АВ равен 13 см, точки А и В лежат на разных окружностях оснований цилиндра. Найдите расстояние от отрезка АВ до оси цилиндра, если его высота равна 5 см, а радиус основания 10 см.
---------------------
АВ и ось цилиндра - скрещивающиеся прямые.
Расстоянием между скрещивающимися прямыми называется
расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
Проведем через АВ плоскость АМВС⊥ основаниям цилиндра.
Искомым расстоянием является длина отрезка ОН, перпендикулярного к плоскости АМВС, содержащей прямую АВ и параллельной оси цилиндра, т.к. АС и ВМ в этой плоскости перпендикулярны основаниям, как и ось цилиндра.
Отрезок АВ - наклонная, поскольку значительно длиннее высоты цилиндра.
Хорда ВС - проекция АВ на основание цилинда.
ВС - высота цилиндра ⊥ основанию.
⊿ АВС прямоугольный - из Пифагоровых троек ( 5
:12
:13), ⇒
ВС=12( можно проверить по т.Пифагора).
∆ ОВС - равнобедренный ( ОС=ОВ=R.)
ОН - высота и медиана ∆ ОВС.
СН=12
:2=
6 см
⊿ ОНС прямоугольный с гипотенузой ОС=10 см и катетом НС=6 см⇒
⊿ ОНС- египетский и ОН=8 см ( по т.Пифагора получим ту же длину)
Расстояние от отрезка АВ до оси цилиндра равно
8 см