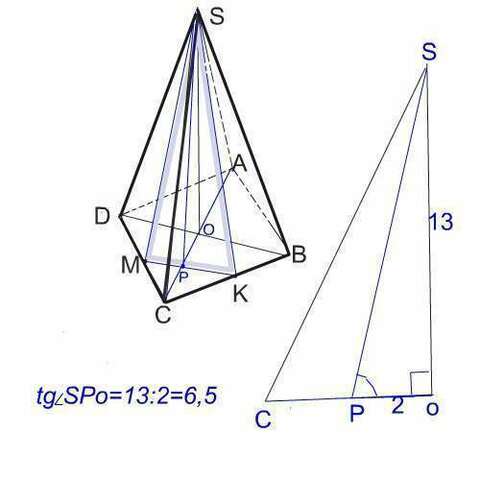
Нарисуем пирамиду, проведем в ней сечение МSK.
МК - средняя линия треугольника CDB, параллельна DB и равна ее половине.
Диагональ АС квадрата АВСD равна диагонали DB
ОР - четверть этой диагонали и равна 8:4=2 (из треугольника CDB, в котором высота делится отрезком МК пополам).
SР- высота, биссектриса и медиана треугольного сечения МSK.
Небоходимо найти tg ∠ SPo, под которым сечение пересекается с плоскостью пирамиды.
Нарисуем отдельно треугольник PSo.
tg ∠ SPo=SP:oP=13:2=6,5