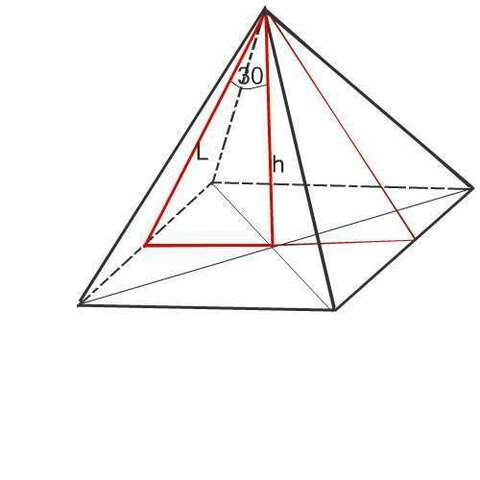
В правИльной четырехугольной
пирамиде площадь полной поверхности
S=1/2PL+S осн (Р - периметр основания)
Сторона основания равна апофеме, так как ее половина противолежит углу 30°, а вся сторона равна, естественно, двум своим половинам. Следовательно, сторона основания ( квадрата) равна L
S основания= L²
Полная площадь правильной четырехугольной пирамиды равна половине произведения периметра ее основания на апофему плюс площадь основания.
S=1/2·4L·L+L²=2L²+L²=3L²
3L²=48
L²=16
L=4
Объем пирамиды равен одной трети произведения ее высоты на площадь основания.
Площадь основания равна 4²=16
Высоту найдем из треугольника, образованного осевым сечением пирамиды через апофемы. Этот треугольник - правильный, так как он - равнобедренный и половина угла при его вершине равна 30°.
Высота правильного треугольника вычисляется по формуле
(а√3):2 в этом треугольнике она равна
(4√3):2=2√3
Объем пирамиды V =1/3 Sh
V=(16*2√3):3 =1/3 ·32√3 cм ³