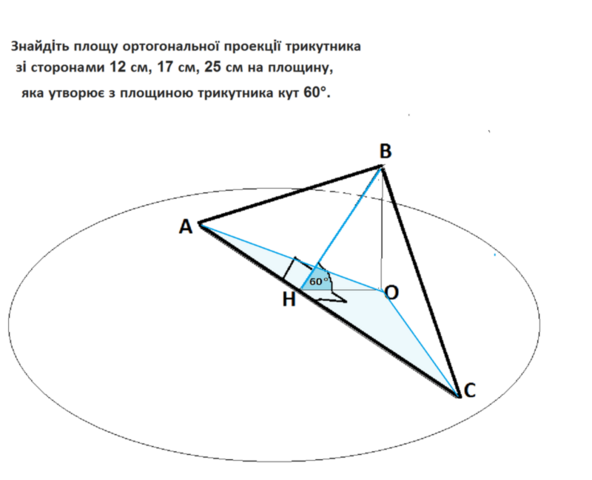
Пусть этот треугольник будет АВС, где основание АС=25 и лежит на плоскости.
Высота ВН треугольника, расстояние ВО от вершины В до плоскости и проекция ОН высоты ВН на плоскость образуют прямоугольный треугольник с углом ВНО=60° по т. о трех перпендикулярах.
Угол НВО=90°-60°=30°⇒
НО=ВН:2.
Отношение площади треугольников с равными основаниями равно отношению их высот.
НО - высота ортогональной проекции данного треугольника на плоскость. Поскольку она проведена к стороне АС=25 и равна половине высоты треугольника АВС,
площадь треугольника АОС равна половине площади треугольника АВС.. Площадь треугольника АВС, найденная по т.Герона, равна 90 см² ⇒
S АОС=90:2=45 см²
--------
Можно произвести расчеты, найдя из площади АВС высоту ВН по формуле:
h=2S:a и затем найти высоту ОН треугольника АОС, после чего - площадь АОС, по которая будет и в этом случае равна 45 см²