По условию AC = 2 * AB, следовательно AB = AC / 2.
Обозначим точку пересечения диагоналей AC и BD параллелограмма ABCD как E.
Точка E делит диагональ AC пополам, следовательно AE = AC / 2 и следовательно AE = AB.
Рассмотрим треугольник ABE. Он равнобедренный, т.к. его стороны AB и AE равны, следовательно углы ABE и AEB тоже равны.
Углы BAE и ACD накрест лежащие, и как следствие равны (и равны 74 градусам, т.к. угол ACD известен по условию).
Найдем углы ABE и AEB. Как известно сумма углов треугольника 180 градусов, следовательно угол ABE = угол AEB = (180 - ACD) / 2 = (180 - 74) / 2 = 53 (градуса).
Таким образом мы нашли один из углов при пересечении диагоналей (угол AEB) параллелограмма ABCD и он равен 53 градусам. Другой угол при пересечении (угол AED) является смежным к этому (к углу AEB) и следовательно равен 180 - 53 = 127 градусов. Оставшиеся два угла при пересечении (углы CED и BEC) являются вертикальными к уже найденным и равны 53 и 127 градусов соответственно. Меньшим из этих углов является угол 53 градуса, что и будет ответом к задаче.
Ответ: 53 градуса.
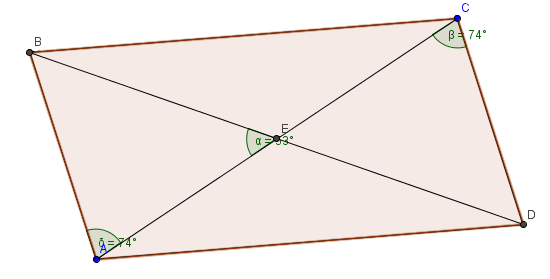
Рисунок: