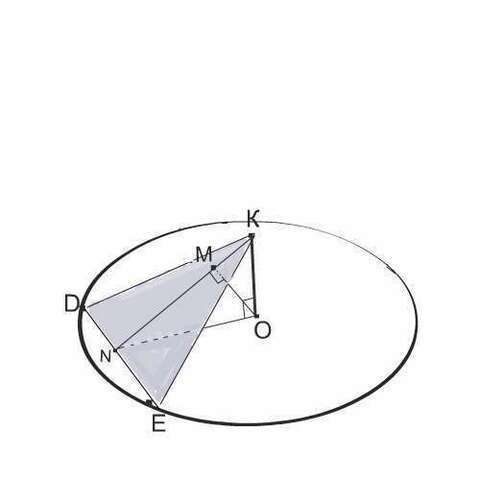
Расстояние от точки до прямой измеряется длиной отрезка, проведенного перпендикулярно из точки к данной прямой.
О - точка, КN - прямая на плоскости сечения.
Решение сводится к нахождению высоты прямоугольного треугольника, проведенной из вершины прямого угла к гипотенузе.
Рассмотрим рисунок.
МО - высота треугольника КОN.
КN= √(КО²+ ОN²) =√(81+27)=√108=6√3
Сравним длину КО и КN.
КО=3√3, КN=6√3
Их отношение -1/2, это значение синуса 30°
Следовательно, ∠ КNО=30°. ⇒
ОМ=NО*sin (30°)=9:2=4,5см