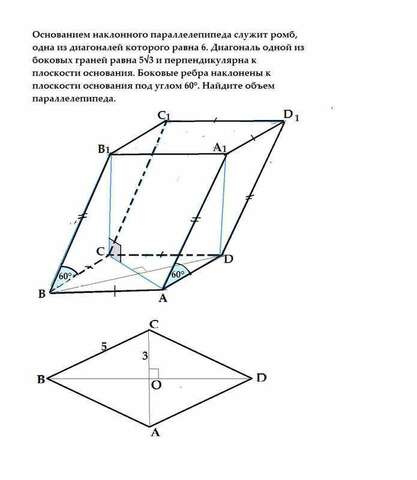
Диагональ В₁С боковой грани ВВ₁С₁С параллелепипеда по условию перпендикулярна плоскости основания и равна 5√3 ⇒ перпендикулярна ВС. Треугольник В1СВ - прямоугольный, угол В₁ВС =60°
В₁В=В₁С:sin (60°)=5√3):(√3)/2=10
Сторона основания ВС - катет треугольника ВСВ₁, противолежащий углу 30° и равна половине длины ребра ВВ₁
ВС=5
Диагонали ромба взаимно перпендикулярны, половина одной из них равна 3 по условию. Треугольник ОВС - египетский,⇒
ВО=4,⇒ ВD=2*ВО=8 (можно проверить по т. Пифагора)
Площадь ромба в основании равна половине произведения диагоналей.
S (ABCD)=0,5*6*8=24
Объем параллелепипеда равен произведению площади его основания на высоту
Поскольку высотой параллелепипеда является отрезок, перпендикулярный основанию, В₁С равен высоте параллелепипеда.
V=24*5√3=120√3 (единиц объема)