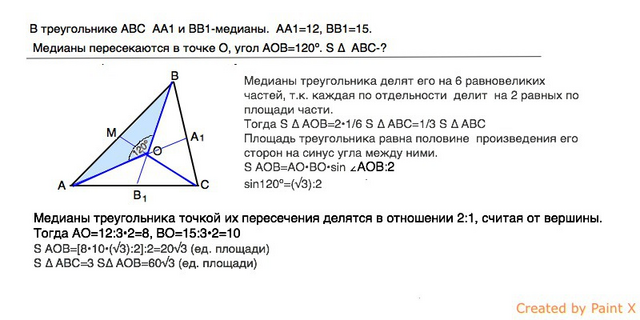
Три медианы треугольника делят его на 6 равновеликих частей, т.к. каждая по отдельности делит на 2 равных по площади части.
Тогда S ∆ АОВ=2•¹/₆ S ∆ ABC=¹/₃ S ∆ ABC
Площадь треугольника равна половине произведения его сторон на синус угла между ними.
S AOB=AO•BO•sin ∠AOB:2
sin120º=(√3):2
Медианы треугольника точкой их пересечения делятся в отношении 2:1, считая от вершины.
Тогда АО=12:3•2=8,
BO=15:3•2=10
S AOB=[8•10•(√3):2]:2=20√3 (ед. площади)
S ∆ ABC=3 S∆ AOB=60√3 (ед. площади)