Радиус окружности, описанной около правильного четырехугольника равен 6√2 см. Вычислите...

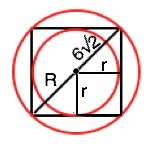
Правильный четырехугольник - это квадрат.

Радиус вписанной в него окружности равен половине стороны. ⇒

а=2r

P=4•2r=8r

C=2πr

P/C=8r/2πr=4/π, и это величина для квадрата постоянная.

По данным задачи:

Радиус окружности, описанной около квадрата, равен половине диагонали квадрата.

Тогда диагональ квадрата 2•R=12√2

Сторона квадрата – катет равнобедренного прямоугольного треугольника с гипотенузой 12√2 и острыми углами 45°

а=12√2•sin45°=6√2•√2:2=12

Р=4•12=48

Радиус вписанной окружности r=12:2=6

С=2•p•6=12π

$\frac{P}C} = \frac{48}{12 \pi } = \frac{4} \pi$