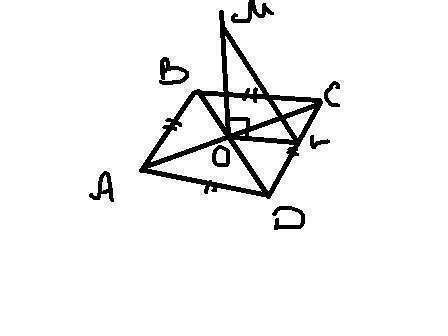
Т.к в ромбе все стороны равны, то для решения задачи можно найти расстояние только до одной стороны ⇒ МL
решение:
МО=5см, МL - наклонная, OL - проекция
1) нам известно, что диагонали ромб пересекаются и делятся пополам
⇒ ОС=АО=30/2=15 , ВО=OD=40/2=20
2) треугольник СОD - прямоугольный (т.к. диагонали пересекаются под прямым углом, т.е. угол COD=90)
⇒ СD - гипотенуза = √15²+20²=√255+400=√625=25
3) ОL - высота
пусть DL = x, тогда LC = 25-x
нам известно, что OL² = DL*LC = x(25-x)
так же известно, что OL² = OD²-DL² = 20²-x²
⇒ если правые стороны равны, то и левые стороны равны, значит
x(25-x) = 20²-x²
25x-x²=400-x²
25x=400
x=400/25=16 - DL
LC=25-16=9
теперь можем найти OL=√16*9=√144=12
4) теперь можем найти ML по т.Пифагора (ML-гипотенуза, OL и OM - катеты):
ML=√5²+12²=√25+144=√169=13
ответ: 13