1. MD = DE по условию,
PD = DK по условию,
∠MDK = ∠EDP как вертикальные, ⇒
ΔMDK = ΔEDP по двум сторонам и углу между ними.
В равных треугольниках напротив равных сторон лежат равные углы, значит
∠KMD = ∠PED.
2. DM = DK по условию,
РМ = РК по условию,
DP - общая сторона для треугольников DMP и DKP, ⇒
ΔDMP = ΔDKP по трем сторонам.
В равных треугольниках напротив равных сторон лежат равные углы, значит ∠MDP = ∠KDP, следовательно
DP - биссектриса угла D.
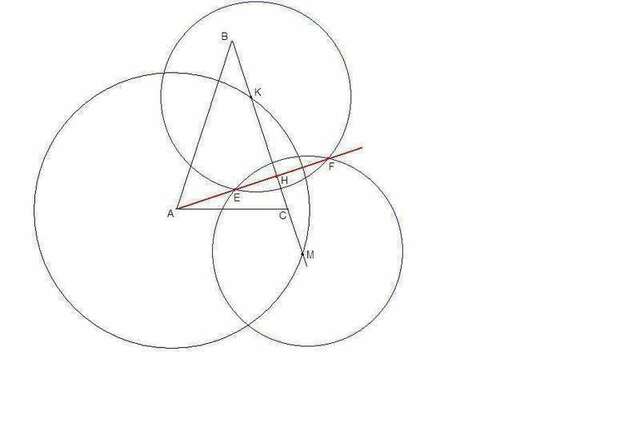
3. Начертим окружность с центром в точке А произвольного радиуса (большего, чем расстояние до прямой ВС). Точки пересечения этой окружности с прямой ВС - К и М.
Начертим две окружности одинакового произвольного радиуса (большего половины отрезка КМ) с центрами в точках К и М.
Через точки пересечения этих окружностей (Е и F) проводим прямую.
EF ∩ BC = H. АН - искомая высота.
Прямая EF всегда пройдет через точку А, так как является серединным перпендикуляром к отрезку КМ, а точка А равноудалена от концов этого отрезка, а значит лежит на серединном перпендикуляре.